Zénon d'Elée.

5 septembre 2018

Le philosophe Zénon soutenait activement les thèses philosophiques de son maître Parménide.

De la province italienne de Salerne, le philosophe Parménide (Grande Grèce, 515 av) affirmait "la réalité immuable de l'Être... et le mouvement comme une illusion". [Lycée International de Saint-Germain en Laye].

> L’arbre de la Connaissance. Détail de la Tapisserie de Bayeux.

Naquit en -490 un des premiers grands philosophe- mathématicien sceptique, Zénon d'Elée. Il fut un zélé disciple de Parménide. De même il affronta le dictateur du moment, Nearchus le tyran, qui sévissait en mer Tyrrhénienne. Il fut emprisonné puis assassiné à l’issu d'une conspiration sans mystère. Reste les titillants paradoxes du fringant agitateur...

La Grande Grèce. La Province d'Elée.

L’Epicheiremate évoque en 200 mots le paradoxe de la dichotomie.
"... Il faut que soit franchie effectivement une série infinie d'étapes, ce qui est impossible... le paradoxe se résout en soutenant que le mouvement est continu... le fait qu'il soit divisible à l'infini ne le rend pas impossible pour autant". [WIKIPEDIA Encyclopédie].

Le paradoxe de la dichotomie.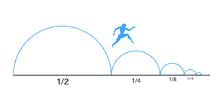
Schéma extrait de l’Encyclopédie WIKIPEDIA.
https://fr.wikipedia.org/ wiki/ Paradoxes de Z%C3%A9non

De même les paradoxes de l’Achille ou de la flèche (du temps) et celui du Stade évoquent des situations paradoxales sensiblement analogues. [Lycée International de Saint-Germain en Laye].

L’Achille s’étant métamorphosé en lièvre galopeur, l'animal velu à grandes oreilles et à queue ronde se trouva confronté à une lente tortue bossue dans une épreuve de course à quatre pattes. Au terme de l'étrange course-poursuite la lente tortue ne fut jamais rattrapée par le rapide lièvre endiablé.

_ C’est de la triche ! On demande au lièvre de viser systématiquement un endroit où la tortue ne se trouvera jamais !

En fait Clopî, il est demandé au lièvre d’effectuer en amont de sa course une division arithmétique itérative. Cette division répétée scinde le champ de course en 2 parties égales...

Deux pièges sont tendus au lièvre galopeur.
De fait la tortue bien que fort lente se déplace constamment...

De plus le calcul mathématique imposé au Lièvre ne possède aucun sens arithmétique; ainsi l'on additionne des distances parcourues à différentes vitesses et l'on divise des longueurs "pures" de terrain; ce qui est une absurdité mathématique.

"Jamais les unités arithmétiques ne mélangeras".

L'Arbre de la connaissance est bien feuillu !

Cependant persiste dans l’ombre de Zénon le mystère des "infinis de division". Ces infinis se matérialisent par la "Suite arithmétique" convergente suivante; 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128… suite dont le terme final tend vers la Grandeur zéro et s'en rapproche indéfiniment sans jamais l'atteindre. Ici réside un paradoxe arithmétique !

Un paradoxe !.. Que nenni, une erreur de calcul.
Ce qui se révèle infini dans ces paradoxes est l'acte de diviser... jusqu’à plus soif, jusqu'à l'épuisement du mathématicien diviseur.

_ C'est vrai au fait ! Quand s'arrête-t-on de diviser une quantité finie ?

Les deux règles élémentaires de l'Arithmétique.

L'unité arithmétique jamais ne diviseras.
L'unité par définition est un minimum infranchissable; un minimum plancher avec rien en-dessous... de plus petit.

L'unité et les Genres jamais ne mélangeras.
Les genres arithmétiques différents; les familles différentes; les domaines différents jamais ne se confondent dans l'univers mathématique.
Aussi Roméo et Juliette ne s'épousent jamais en Pays d'Arithmétique.

L'Unité = l'insécable, l'élémentaire, le minimum... l'indivisible.

L'Arbre de la connaissance nous semble bien dru et peu cru !

L’unité arithmétique.

L’unité précise l'élémentaire et se définit par sa valeur minimum "plancher". Aussi n’y a-t-il rien de plus petit que la "Quantité unité".

Le Quantum conçu en 1900 par le physicien Max Planck impose un minimum indivisible; le quantum minimum d'énergie ou d'action.
Ce quantum est l'unité arithmétique d'énergie ou d'action.

Sur la droite numérique, zéro précède 1 d'une unité. (Dana MACKKENZIE. Mathématicien. Université de Princeton).

_____0___________________1______________

… en analyse moderne, le paradoxe (de Zénon) se résout en invoquant le fait qu'une série "infinie" de nombres strictement positifs peut converger vers une grandeur finie… ainsi additionner une infinité d’éléments "de plus en plus petits" abouti à un résultat fini. (Dana Mackenzie-Mathématicien).

L'Opérateur de fractionnement. Se distingue de l'acte de diviser celui de fractionner.

Les Opérateurs arithmétiques, les acteurs mathématiques tels que l'addition, la soustraction, la multiplication et la division opèrent et jonglent avec les unités arithmétiques. Dans ces calculs les unités arithmétiques sont constituées à priori, en amont des calculs.

Le Jardin d'Eden.

A l'inverse de la division le fractionnement est un Opérateur qui fait cavalier seul. Ainsi le calcul fractionnel interprète une partition "solo" et jongle uniquement avec des "unités" de Taille infinitésimale. De la "fraction infinitésimale" résulte la Taille de l'unité infinitésimale et le calcul de ses multiples.

Ainsi l'acte de fractionner est philosophiquement l'inverse de l'acte de diviser; ainsi deux frères jumeaux subtilement inverses et cependant complémentaires.

Dom ROBERT. Tapisserie du XXe siècle. Château de BOUSSAC. Aubusson. Le Jardin d'Eden.

Le discours arithmétique introduit la notion de "tendre vers la limite", voire de "passer la limite". La limite est la "Grandeur minimum" définissant la Taille de l'unité infinitésimale active dans son Domaine. Aussi les séries arithmétiques convergentes tendent vers la valeur de l'unité.... et s'arrête quand.... il n'y a plus rien à diviser. L'unité défini la valeur butoir indivisible; la valeur minimum indépassable.

Ainsi meurent les Infinis de division, fracassées par l'Infinitésimal butoir.